Числа: раціональні, дійсні, комплексні – що стоїть за цими словами? Як ми розуміємо кількість?

У своїй статті “Чому варто довіряти науці?” я коротко описав особливості наукового пізнання, що роблять його успішнішим за альтернативні світогляди та допомагають неспеціалістам відрізнити його від “підробок”. У ній левову частку уваги я приділив тому, як у дослідах перевіряються різні моделі світу, що пропонуються науками.

Лишається одне дуже цікаве питання — а звідки в науках беруться різні моделі? Цей процес ніхто не формалізував і навряд чи зможе, бо це справа творча. Однак найближчою до відповіді на це запитання є одна область людських знань — математика. Вона оперує такими абстрактними поняттями, як числа, точки, вектори, котрих не існує в природі. Однак логічне доведення тверджень, яке вона пропонує, є дуже ефективним способом вирізнити багато помилкових тверджень на “початковому етапі” досліджень.

Думаю, що поняття, упроваджені математикою, хоча вони і є ідеалізованими наближеннями, слід уважати реальними в тому сенсі, що вони придатні для опису дійсності в рамках зовсім різних наук. Наприклад, статистичні формули, що беруться з теорії ймовірностей, використовуються як у ядерній фізиці, так і в соціології. Диференційні рівняння використовуються як в описі руху деталей механічних приладів, так і в макроекономіці для опису поведінки ринку. Вектори та матриці використовуються як в описі руху тіл складної форми, так і в машинному навчанні чи аналізі даних. Цей перелік можна продовжувати дуже довго, та математичні формули завжди однакові і не залежать від того, де вони зустрічаються. Як на мене, це достатньо вагома причина, щоб на математику варто було звернути увагу всім, незалежно від роду заняття.

Зараз пропоную зосередитися на одному понятті, яке першим приходить до голів більшості людей, коли вони чують про математику. Це поняття числа́. На перший погляд, тут усе просто — число це те, що означає кількість, є відповіддю на питання “скільки?”. Однак ми можемо оце “скільки” визначати в різні способи. Щоб урахувати всі ці можливості, нам доведеться розширювати множину чисел. Пропоную простежити за цим процесом разом.

Натуральні та цілі числа

Числа виникають, коли ми починаємо рахувати. Множину чисел, які ми використовуємо для рахування  ^, математики називають натура́льними числами. Вона є нескінченною, оскільки як багато об’єктів ми би собі не уявили, завжди можна помислити кількість принаймні на один більше. Відповідно, можна сказати, що після кожного натурального числа є якесь наступне число, а за ним ще одне і так далі.

Однак рахунок — це не єдиний спосіб визначити кількість. Ми можемо визначати одні кількості через інші і так приходимо до поняття арифмети́чних опера́цій. Результат їх виконання теж означає кількість, отже, наше поняття про числа має його враховувати. Почнемо з додавання. Коли ми додаємо два будь-яких натуральних числа, то результат теж є натуральним числом. Так само і з множенням. Це називається повнотою множини натуральних чисел відносно додавання та множення.

Коли ми введемо також обернені операції — віднімання та ділення, усе ускладнюється. Якщо ми від більшого числа віднімемо менше, то результат буде натуральним числом. Результат віднімання числа самого від себе — це нуль¹ , число, що означає відсутність кількості. Для позначення результату віднімання більшого числа від меншого математики ввели від’ємні числа, їх записують зі знаком мінус (Ті числа, що нам уже були відомі, на противагу називають додатними). Ці нововведення розширюють множину чисел до ці́лих . Якщо додати якесь додатне число і протилежне йому від’ємне (таке саме, тільки з мінусом), то отримаємо нуль. Якщо додамо до будь-якого числа нуль, отримаємо те саме число.

Слід зауважити, що множина цілих чисел є зліче́нною. Так у математиці називаються множини, для перерахування елементів котрих “вистачить”² натуральних чисел. Ми можемо “порахувати” цілі числа виставивши їх, наприклад, у такому порядку:  Отже хоча нам здається, що цілих чисел “удвічі більше” ніж натуральних через наявність від’ємних чисел, однак ці дві множини дві є “однаково нескінченними”. Пізніше ми розглянемо приклад нескінченної множини з більшою — як кажуть математики — поту́жністю.

Раціональні числа

Після того, як вирішено ситуацію з відніманням ³, занепокоєння викликає ситуація з діленням. Справа в тому, що не всі цілі числа діляться на інші цілі числа до решти. Значить є ще якісь нецілі числа, які ми будемо впроваджувати через ділення. Будемо записувати ці числа у вигляді дробів: — один поділити на два, — три поділити на п’ять, тощо. Верхнє число у дробі називається чисельником, а нижнє — знаменником. Одне і те саме число можна представити багатьма способами: можна помножити чисельник і знаменник на будь-яке ціле число — і отримаємо “синонімічний” дріб.  Якщо можна поділити чисельник і знаменник на одне і те саме ціле число до решти, то цей процес називається скороченням дробу. Значення дробу при цьому не змінюється. Загальноприйнятим є запис чисел у вигляді нескоро́тних дробів, але інші дроби також є допустимі. Якщо після скорочення виявляється, що знаменник є одиницею, значить число є цілим (отже таке представлення включає в себе цілі числа).

Якщо взяти дріб і поміняти місцями чисельник зі знаменником, то отримаємо число, що називається обе́рненим. Добуток будь-якого числа на обернене до нього дорівнює одиниці. Будь-яке число помножене на одиницю дорівнює собі. Це нагадує ситуацію з нулем і додаванням.

Зупинимося ще на питанні знаку таких чисел. Якщо і чисельник, і знаменник будуть від’ємними числами, то дріб скорочується на -1 і відповідно представляє додатне число (мінуси зникають). Якщо в дробі мінус тільки один, то це є від’ємне число.

Описані вище числа називаються множиною раціона́льних чисел (позначається символом ). Вона є повною відносно додавання, віднімання, множення та ділення (окрім ділення на нуль).

Цікавим та неочевидним є факт, що множина раціональних чисел також є зліченною. Один з прикладів, як можна “порахувати” додатні раціональні числа, показано на цій схемі:

дроби, що виділені червоним кольором, скорочуються і є представленням чисел, що вже були “на маршруті”. Пропоную читачеві самостійно включити до “маршруту” від’ємні числа та переконатися, що вся множина раціональних чисел є зліченною.

Піднесення до степенів

Тривалий час множина раціональних чисел влаштовувала математиків. Однак перелік математичних операцій розширювався, і відповідно люди змогли подумати про нові цікаві числа, які не можна визначити через відношення (дроби).

Найпростіша операція, що може спонукати нас до подальшого перегляду поняття чисел — це підне́сення до сте́пеня. Записують цю операцію, використовуючи верхній індекс: після числа, яке підносять до степеня (основи), угорі пишуть число, що є показником степеня — ось так “15³”.

Почнемо з випадку, коли показник є натуральним числом. Тоді степенем є добуток основи самої на себе стільки разів, скільки записано в показнику. Квадрат числа — це другий степінь x²=xx, куб — третій степінь x³=xxx, вищі степені не мають таких загальновживаних назв. Число в першому степені — це воно саме: x¹=x.

Поки що все чудово, оскільки піднесення до таких степенів не породжує незнайомих нам чисел. Розширюючи поняття степеня на інші показники, будемо домагатися того, щоб піднесення до степеня зберігало свої основні властивості⁵, які в нього є на даному етапі:

• поведінка при додаванні показників: x^a+b=x^ax^b

• поведінка при множенні показників: x^ab=(x^a)^b

• поведінка при множенні основ: (xy)^a=x^ay^a

Щоб розширити визначення до цілих показників, скористаємося першою властивістю: 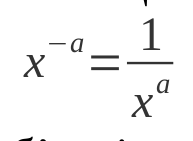 та визначимо нульовий степінь⁴ як одиницю x⁰ = 1. Це теж не породжує дивних об’єктів.

Однак коли ми скористаємося другою властивістю степеня і впровадимо нецілі показники, то на нас чекатимуть проблеми вже на самому початку.

Дійсні числа. Континуум

Упроваджуючи нецілі показники степенів ми стикаємося з проблемою вже на дуже простому прикладі. Візьмемо степінь , який ми зі школи знаємо як квадратний корінь. Фактично це є операція обернена до піднесення до степеня 2 (квадрату). Корінь навіть для такого звичайного числа як 2 не може бути представленим у вигляді дробу. Він є числом ірраціона́льним. Відкриття їх у математиці пролило світло на проблеми, що не вирішувалися протягом століть. Бодай найвідомішою з них була задача про квадрату́ру кру́га.

Щоб представити ірраціональні числа, згадаймо зі школи десятко́ві дро́би. Раціональні числа відповідають або скінченним, або нескінченним періодичним десятковим дробам. Однак існує також сила-силенна нескінченних неперіодичних дробів — а отже чисел, які вони представляють. Це і є ірраціональні числа.

Уся множина чисел, які тепер доступні нам для представлення, називається ді́йсними чи́слами (позначається як ). Їх настільки багато, що вони є незліченною множиною. Щоб проілюструвати це, скористаємося числово́ю прямо́ю — це геометричне представлення множини всіх дійсних чисел, де кожному числу відповідає якась точка на прямій. І які би ми не обрали дві точки-числа на цій прямій, як би вони не були близько одна до одної, між ними знаходиться нескінченно багато точок-чисел. Нескінченні множини, що мають таку потужність, називають конти́нуум. Як дивує те, що множини цілих і раціональних чисел є зліченними, так само дивує, що в будь-якому інтервалі, наприклад від 0 до 1, міститься настільки ж “багато” чисел, як і на всій числовій прямій. Такі дивні властивості мають нескінченні множини!

Декому всі ці обмірковування щодо нескінченності можуть здаватися лише “цікавою математичною іграшкою”, однак можу сказати, що в багатьох розділах фізики математичні властивості нескінченних об’єктів використовують для опису зовсім конкретних явищ. Приклад, який вам охоче наведуть навіть студенти 3 курсу, це інтеграли по нескінченних областях, які можуть бути скінченними і відповідати фізичним величинам, які можна виміряти. Нескінченність — це лише один приклад того, наскільки тісно всі ці “математичні іграшки” переплетені зі світом навколо нас.

Дуже часто нові поняття в математиці виникають самі собою, лише через те, що ми можемо таке помислити. Однак пізніше виявляється, що ці нові об’єкти чудово підходять для опису явищ з реального світу. Як на мене, це є головним прагматичним аргументом на користь переконання, що математичне знання є об’єктивним.

Уявна одиниця. Комплексні числа

Розширення множини всіх чисел до континууму вирішило багато проблем. Дійсні числа придатні для точного опису різного роду явищ і їхній зв’язок з реальністю очевидний для багатьох. Однак в цієї множини чисел є одна проблема щодо повноти відносно піднесення до степенів. Найпростіший приклад — це відсутність квадратних коренів у від’ємних чисел.

Що ж, можна просто вигадати таке число i, якого немає на числовій прямій та квадрат якого дорівнює -1. Такий об’єкт називається уя́вною одини́цею. Квадратні корені інших від’ємних дійсних чисел становитимуть інші уявні числа, що виражаються через i (згадаймо властивості піднесення до степенів). Наприклад: , ,   тощо.

Упроваджуючи можливість додавати і віднімати дійсні та уявні числа, ми розширюємо наше “поле діяльності” до множини ко́мплексних чи́сел (позначають як ), яку можна представити у вигляді площини:

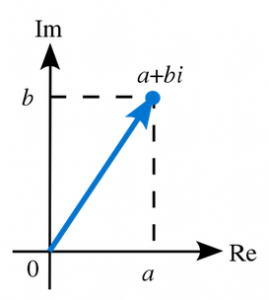
Координати на цій площині відповідають дійсній (Re) та уявній (Im) частинам комплексних чисел.

Така множина є повною відносно всіх чотирьох арифметичних операцій:

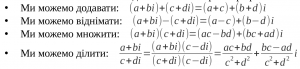
Користуючись тими самими правилами, якими у школі спрощували вирази, ми завжди в результаті отримуємо комплексне число.

Представляючи комплексні числа точками на площині, так само як у геометрії переходять від дека́ртових координа́т до поля́рних, ми можемо впровадити альтернативну форму запису:

c = a+bi = r cosφ+ir sinφ,

де r — це відстань від точки, що представляє наше число, до нуля (початку координат), а φ — кут між напрямком на наше число та віссю дійсних чисел.

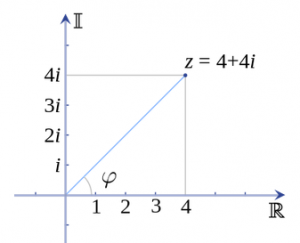
Цікаві речі виникають, коли ми починаємо підносити комплексні числа до степенів. На етапі впровадження цілого показнику степеня можна отримати таке співвідношення: rⁿ (cos φ + i sin φ)ⁿ = rⁿ cos( nφ ) + i rⁿ sin ( nφ ), яке є фо́рмулою Муа́вра.

Узагальнюючи піднесення до степенів до комплексних показників, математики отримали гарне та корисне співвідношення e^iφ = cos φ + i sin φ, де e — це відоме число́ Е́йлера (дійсне число, яке є настільки цікавим, що могло б стати матеріалом статті суттєво більшої за цю). Ця формула пов’язує комплексні числа з тригономе́трією та дає ефективний інструмент для опису періодичних процесів.

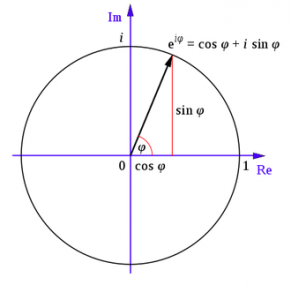
Комплексний аналіз є яскравим прикладом того, як вигадані математиками об’єкти виявляються пов’язаними між собою простими співвідношеннями. Часто мислителі також пов’язують математику з уявленнями про прекра́сне. Однак найбільш вражає те, що ці “вигадані” числа стали інструментом опису широкого кола явищ у різних галузях: фізиці, хімії, економіці, теорії керування тощо.

Примітки

1. У деяких математичних працях множину натуральних чисел визначають так, що вона теж містить нуль.
2. Тут і далі для простоти сприйняття я метафорично використовую для нескінченних множин слова “менше”, “більше” і подібні їм так, як для скінченних. Я беру їх у лапки, щоб було видно, що це не є строгим математичним терміном.
3. Насправді математики спочатку розширили множину натуральних чисел, кажучи сучасною мовою, до множини додатних раціональних чисел (її іноді позначають як Q⁺), а потім уже впровадили поняття від’ємних чисел. Однак сучасні математичні визначення множин чисел спочатку вводять множину цілих чисел, а потім розширюють її до множини раціональних чисел — так зручніше.
4. Не існує загальноприйнятого визначення, що таке 0⁰.
5. Узагалі такого роду властивості є і в чотирьох арифметичних операцій, які відомі нам ще зі школи. Для додавання це: a+b= b+a; a+(b+c)=(a+b)+c . Для множення: ab=ba; (ab)c = a(bc); (a+b)c = ac+bc.  З цих формул можна вивести властивості віднімання та ділення — обернених операцій. Коли ми розширювали множину чисел, починаючи від натуральних, ми теж домагалися збереження цих властивостей, але в тексті я на цьому не акцентував уваги, уважаючи це очевидним, на відміну від піднесення до степенів.
6. У цій статті використані ілюстрації з україномовної версії сайту Вікіпедії

Що почитати зацікавленим:

Roger Penrose — The road to reality. A complete guide to the laws of universe

Edward Frenkel — Love and math

Martin Gardner — Penrose tiles to trapdoor ciphers

Повний список моїх математичних статей:

• Числа (цілі, раціональні, дійсні, комплексні)
• Математичний простір. Скаляри та вектори
• Імовірності. Розподіли. Статистика. Похибка
• Трансцендентні числа. Математичні ряди. Наближені обчислення
• Послідовності. Прогрессії. Відсоткова ставка кредитів