Коли мінус на мінус не дає плюс навіть в математиці
29 Липня 2019 | Олексій Ігнатенко
Категорія: Математика
Теги: додавання, математика, множини, натуральні числа
Про елементарні операції і їх розуміння. Про числа і множини і про те, що трапляється, коли робиш крок у невідоме. Що робити, якщо ви опинились у невідомому просторі множин і з чого почати його облаштування? Як додавати і головне віднімати множини, щоб це мало сенс.
Для мене задача вирішена в той момент, коли вона поставлена.
Джон Ф. Неш, математик, лауреат Нобелівської премії
Вступ
Математичні конструкції і формули часто відлякують від читання, особливо це стосується науково-популярної літератури. І дійсно, невже не можна обійтись без них? Стівен Гокінг колись сказав, що кожна формула зменшує кількість читачів вдвічі (це стосувалось лише науково-популярної літератури!) і спочатку залишив в своїй “Короткій історії” одну-єдину Е=mc2, а потім, в черговій редакції, викинув і її. Уникнення формул стало трендом і, мабуть, мейнстрімом. І це, можливо, прийнятно в багатьох областях – біології, археології, фізиці – але не в математиці. Справа в тому, що формули є абстракціями, які дозволяють швидко оперувати загальними категоріями. Завдяки цим символам можливо формулювати ідеї та будувати складні конструкції. Формульні структури утворюють спільний простір, в якому математики можуть спілкуватись незалежно від їх мови. В цій статті я спробую показати на дуже простому прикладі, як такі структури виникають та за якими законами вони розвиваються (і постараюсь майже без формул).
Коли все начебто очевидно просто, але ніт
Всім відомий вираз “мінус на мінус дає плюс” і його значення. Формульно він записується дуже коротко:
– (- а ) = + а
а ідея в тому, що мінус – це щось “погане”, але іноді комбінація поганого і поганого дають в результаті щось “хороше” – плюс.
Як правило, плюс перед числом не пишуть, але важливо пам’ятати, що він там є. Зрозуміло, що мінус без плюса не має сенсу, отже потрібно почати з цієї елементарної операції. Для того щоб пройти шляхом абстрагування, потрібно згадати, як взагалі будуються числа й здійснюються операції над ними? Спочатку потрібно визначити базовий елемент – це може бути будь-що: наприклад, стілець.

Один стілець (базова одиниця)
Якщо у нас є стілець, то ми можемо поставити поруч ще один (уявімо собі, що в нас їх нескінченний запас) і ця можливість вже визначає всі натуральні числа.
 +
+ 
Один стілець і ще один стілець (ідентичний першому)
Важливо зробити крок до абстрактної кількості стільців. Хоча це цілком очевидно для нас, далеко не всі народи в історії змогли зробити цей крок. Відомі племена, які зупинялись на визначенні понять “один, два, багато” або ті, які мали окремі чисельники для округлих, квадратних та лінійних предметів – бо як можна додуматись додавати дерева і оленів? Але коли ми зробили крок до додавання кількості об’єктів, операція суми цілком інтуїтивно зрозуміла – потрібно поставити стільці поруч і сказати: ось два стільці. Отже стілець і стілець – тобто сума цих стільців 1 + 1 = 2. В принципі, позначати окремим символом результат необов’язково, але це суттєво економить час. Цей крок можна, наприклад, спостерігати у австралійських племен, у яких числа на момент приходу європейців мали такий вигляд (плем’я Каміларої): 1 = мал, 2 = булан, 3 = гуліба, 4 = булан-булан, 5 = булан-гуліба, 6 = гуліба-гуліба.
Таким чином, ми можемо отримати будь-яке натуральне число, просто додаючи одиницю:
1 + 1 + 1 = 3, 1 + 1 + 1 + 1 = 4, …
При цьому ми використали поки що лише один (стілець), операцію додавання й загальну ідею абстрагування. Чому це важливо? Тому що одна проста операція (правило додавання) утворила цілий простір чисел, який вже починає існувати за власними законами. Наприклад, цей простір необмежений, не існує найбільшого числа оскільки до нього завжди можна додати ще одиницю.
Наступний принципово важливий крок – знаходження елементу, який був би “нейтральним” відносно операції. Тобто, це має бути такий “стілець”, щоб його сума з будь-яким числом не змінювала це число. Для операції додавання традиційно такий елемент називається нулем. Його поява (можливо в Месопотамії, можливо в Індії) була дійсно науковим проривом – адже з практичної точки зору вводити окремий символ для позначення пустоти досить дивно. Цей винахід зробив можливою десятичну позиційну систему числення, яка через арабів потрапила до Європи (тому і арабські числа). Додавання нуля записується наступним правилом:
0 + а = а + 0 = а
Поки що все чудово й узгоджено. Є нуль і натуральні числа (деякі математики вважають нуль натуральним, деякі – ні), сума дозволяє отримувати нові числа з існуючих і не виводить за межі простору. Тобто, неможливо, додаючи натуральні числа, отримати ненатуральне число.
Але в цей числовий рай потрапляє змій сумнівів і питань. От наприклад, яке число потрібно додати до 3, щоб отримати 5? Можна підібрати це число напряму: 2 + 3 = 5, а можна відняти від 5 (стільців) 3 (стільці) і отримати той же результат. Очевидна штука, але її ефект прихований і руйнівний. Ми щойно ввели нову операцію, обернену до додавання. І вона виводить за межі нашого відомого простору чисел! Щоб це зрозуміти достатньо спитати: а яке число потрібно додати до 5, щоб отримати 2? Це число -3 і мінус тут є частиною числа. Так, це число пов’язане з відомою нам трійкою певним співвідношенням, але по суті від’ємні числа – це окремий клас. Тобто,
-3 = 0 – 3
Або інакше: -3 це таке число, яке при додаванні до 3 дасть 0. Множина всіх таких чисел (додатніх і від’ємних) називається цілими числами. Цікавою є геометрична інтерпретація, числа 3 і -3 симетричні відносно нуля, тобто операція 0 – 3 це те саме, що відобразити 3 відносно нуля (помножити на -1). Подвійна симетрія повертає точку саму в себе, саме тому для чисел у виразі “мінус на мінус дає плюс” немає нічого дивного.
Як одна операція та інтуїтивне бажання узагальнювати створюють нові простори.
Послідовність кроків, яку ми щойно зробили повторюється при введенні множення. Множення – це, по суті, сума сум чисел, і в стародавньому Єгипті, де не було позиційної системи запису чисел, це суттєво використовували. Відомий приклад множення 11 на 13, якому вже під 4000 тис. років. Папірус пропонує знаходити відповідь наступним чином. Запишемо 13 = 1 + 4 + 8, потім зведемо до додавання та множення на два:
*1 11
2 22
*4 44
*8 88
Тепер додаємо числа в рядках з зірочками і отримуємо результат – 143.
Оберненою операцією до множення є ділення. Ділення виводить за межі цілих чисел і його необхідно розширити. Наслідком є виникнення раціональних чисел (тобто чисел виду m/n, де m, n – натуральні).
Але і це не все, бо ще є піднесення до квадрату (множення множень), яке також має обернену операцію – видобування кореню. Видобування кореню знов таки виводить за межі простору, доводиться розширювати його до комплексних чисел. А далі ще є поле кватерніонів… Як видно, узагальнення – це залежність, іноді важко зупинитись. Ці нові простори можуть бути дуже різні, але для всіх виконується правило, що мінус – це симетрія відносно нуля. Тому мінус від мінуса таки плюс (те саме число), хоч для дійсних, хоч для комплексних. Множення цю властивість вже втратило, тому корень кореня це корень 4 степеня а не саме число (є виключення – одиниця).
Однак узагальнювати можна не лише в напрямку введення нових операцій: що буде якщо замість однієї точки ми розглянемо множини точок?
Вихід у невідомий простір. Вітаю в просторі множин.
Множини є дійсно фундаментальним поняттям в математиці. І, завдяки Рене Декарту, ми можемо зв’язати числа і множини. Кожне число є точкою на осі, то чому б не розглянути множини точок, або, скажімо, відрізки? Невже щось зміниться якщо ми будемо додавати не числа а множини?
NB. Тут потрібно зробити невеликий відступ. Якщо математики переносять стару, відому операцію на новий простір, то вони мають це відповідно обгрунтувати. Якщо це сума, то вона має відповідати властивостям суми, або називатись по іншому. Особливо це стосується ситуації, коли старий простір є частиною нового. Тоді операція має перетворюватись на звичну операцію на старому просторі, інакше виникне плутанина.
Розглянемо спочатку множину, яка складається з відрізку [1,2]. Як розуміти додавання [1,2] + [1,2] (не плутати з об’єднанням множин, де ми просто беремо точки однієї множини і дописуємо точки іншої)? Герман Мінковський, німецький математик (відомий тим, що ставив трійки Альберту Ейнштейну), запропонував такий спосіб: візьмемо всі можливі пари точок з цих множин і знайдемо суму окремо кожної пари. Як додавати окремі точки ми знаємо. А потім об’єднаємо результати в одну множину. Ця операція отримала назву сума Мінковського (але іноді її називають просто сумою множин). Формульно це записується просто:
X + Y = {z ∈ Rn: z = x + y, x ∈ X, y ∈ Y}

Праці Мінковського щодо загальної теорії відносності нещодавно видані окремою книгою [1].
Спочатку спробуємо додавати множини в одновимірному просторі. Найпростіша множина з двох точок {-1,1}, додамо її до самої себе:
{-1,1} + {-1,1} = {-2, 0, 2}
Тут ми утворили пари -1 -1, -1 1, 1 -1, 1 1 і знайшли суми для кожної пари.
{-1,1} + {-1,1} + {-1,1} = {-3, -1, 1, 3}
{-1,1} + {-1,1} + {-1,1} + {-1,1} = {-4, -2, 0, 2, 4}
Щось не дуже схоже на числа. Спробуємо додати відрізок [1,2]:
[1,2] + [1,2] = [2,4]
[1,2] + [1,2] + [1,2] = [3,6]
[1,2] + [1,2] + [1,2] + [1,2] = [4,8]
Це вже схоже на додавання чисел, чи не так? Адже [2,4] = 2*[1,2], якщо множення розуміти аналогічно додаванню. Але вже з першого прикладу зрозуміло, що X + X ≠ 2X для довільної множини.
Ще один приклад, коли X + X ≠ 2X ([2]):
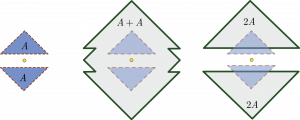
Ще один цікавий приклад: що можна сказати про множину X, для якої виконується X + X = X? Для чисел відповідь очевидна – це може бути тільки нуль. А от множин таких нескінченно багато. Дійсно, візьмемо множину всіх цілих чисел {…-3, -2, -1, 0, 1, 2, 3,…}, для неї властивість виконується. Візьмемо будь-яке ірраціональне число, нехай це буде π. Помножимо його на кожне ціле число – {…-3π, -2π, – π , 0, π, 2π, 3π,…}, для цієї множини також X + X = X.
Навіть якщо ми введемо додаткове обмеження щоб множина Х була опукла. (опуклість означає, що вона завжди містить відрізок який сполучає дві будь-які її точки. На числовій прямій опуклими множинами є відрізки або півнескінченні інтервали), то таких множин на числовій прямій буде рівно шість (чи зможете ви їх знайти?).
Спробуємо тепер додати множини на площині. Виявляється, що найпростіше додавати круги (нагадую, що круг – це точки площини, обмежені колом). Якщо взяти два круга, то їх сума теж буде кругом з центром у сумі центрів і з радіусом рівним сумі радіусів. Цей елегантний результат дає інтуїтивне очікування, що операція має сенс.
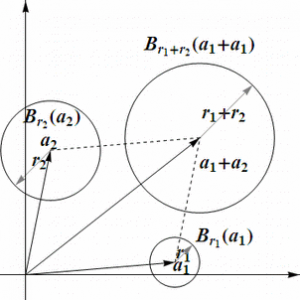
Схожа ситуація відбувається при додаванні однотипних квадратів, трикутників і т.д. А що буде при додаванні квадрата і круга?
Результатом буде такий квадрат з “згладженими” кутиками (його границя виділена червоною лінією). Додавання різних фігур у двовимірному та тривимірному просторі можна глянути в презентації [3].
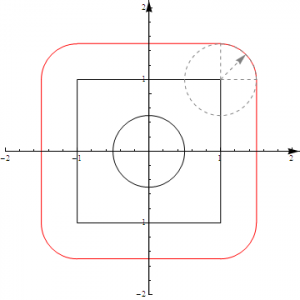
Але якщо додавання ще можна дещо зрозуміти, з відніманням справжня катастрофа. Спробуємо спочатку очевидний шлях – поточкове віднімання (так само як ми зробили з сумою):
[-1,1] + [-1,1] = [-2,2]
[-1,1] – [-1,1] = [-2,2]
Виходить, що X + X дає той самий результат, що і X – X? Так, і це виконується для всіх симетричних відносно нуля множин (пам’ятаєте, що мінус – це симетрія), тобто, якщо множина симетрична, то –X = X. Якась Орвеллівська математика виходить: свобода – це рабство, мінус – це плюс.
Різниця Мінковського.
Простір множин (ми будемо тут говорити лише про компактні множини, ті які можна вписати в кулю й у них суцільна границя, без дірок) виглядає як числовий простір – є сума й множення на числа. Для них виконуються багато властивостей, звичних нам з простору чисел. Але віднімання і множення на від’ємні числа інші. Мінковський, який одним з перших досліджував ці простори, запропонував дуже дивну операцію. Пам’ятаєте, на початку ми визначали -3 як число, яке потрібно додати до 5, щоб отримати 2? Мінковський використав схожу ідею. Якщо нам потрібно знайти X -* Y (де дивний значок -* означає різницю Мінковського), то спробуємо знайти таку множину Z, щоб Z + Y була підмножиною X (для множин рівність виконується рідко, довелось використати оператор підмножини). Формульно це довге визначення записується так:
X -* Y = {z ∈ Rn: z + Y ⊂ X}
Спробуємо відняти від великого червоного круга (позначимо A) маленький синий круг (позначимо B). Якщо до круга з центром в нулі додати точку – вийде круг з центром в цій точці. Отже нам потрібно знайти всі точки, такі щоб синій круг, перенесений в цю точку, не виходив за межу червоного.
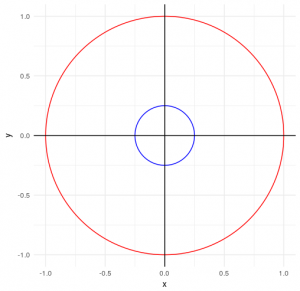
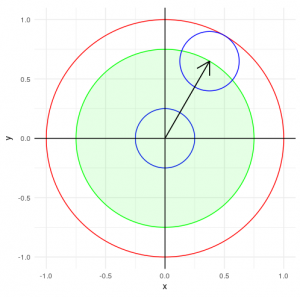
Отже різниця Мінковського двох кругів (з центром в нулі) теж буде кругом (позначений зеленим) а його радіус буде дорівнювати різниці радіусів – більший мінус менший. Тепер спробуємо додати до результату круг, який ми віднімали: виходить, що A -* B + B = A. Також виконується, що різниця Мінковського двох однакових куль буде дорівнювати множині, яка містить лише точку 0. А це вже зовсім схоже на числа. На жаль, так красиво виходить лише з кругами (і лише коли вони з центром в нулі), але загалом це набагато краще ніж те, що було. При цьому важливо, що різниця Мінковського для чисел (одноточкових множин) співпадає зі звичайною різницею.
Сума і різниця Мінковського мають багато чудових властивостей. Ці операції є основою опуклого аналізу, дослідження багатозначних відображень і диференціальних включень. Є й більш практичні застосування для обробки зображень[4] та алгоритмів уникнення зіткнень у робототехніці[5].
Замість епілогу
Повертаючись до початкової фрази: виходить, що мінус на мінус дає плюс, тільки коли ми звужуємо наше багатогранне життя до чисел – одноманітних, одноточкових множин, а операцію – до суми. Цікаві питання, які можуть спасти на думку при читанні цієї статті:
- Чи існують від’ємні множини?
- Що таке добуток множин?
- Що таке корень з множини?
- Чи можна множину піднести до степеню множини?
- Залишимо їх відкритими.
Література
[1] Minkowski, H. (2012) Space and Time Minkowski’s Papers on Relativity. Ed.: Petkov, V., Minkowski Institute Press, Moscu. http://rgs.vniims.ru/books/spacetime.pdf dq=inauthor:%22Hermann+Minkowski%22&hl=uk&source=gbs_navlinks_s
[2] https://en.wikipedia.org/wiki/Minkowski_addition
[3] Minkowski Sums: definition, complexity, construction, applications. Efi Fogel Tel Aviv University, Israel. Algorithmic Robotics and Motion Planning March 14th, 2011
[4] https://en.wikipedia.org/wiki/Erosion_(morphology)
[5] Ericson, Christer. Real-time collision detection. CRC Press, 2004.
Заголовне фото “Chess Board, External Transparency, Both Poles Showing, Droste Effect” авторства Josh Sommers позичене на сторінці Flickr





Обговорення
29 Липня 2019, 21:30
Чудова стаття. Сподіваюся, що буде продовження.
Думаю, що дуже актуальною була б стаття, що пояснює властивості різних множин чисел (натуральні-цілі-райіональні-дійсні-комплексні) та навіщо математики їх розширюють.
Також доречними були би статті про геометрію, що пояснювали би базові речі, а можливо навіть розповідали про неевклідові геометрії. Я трошки зачіпав геометрію в своїх текстах про теорію відносності, але таких пояснень з нуля на сайті ще немає.
Пропоную співпрацю.
29 Липня 2019, 22:42
Дякую. Про числа і їх розширення – більше до алгебраїстів (в мене інша область). Як буде вільний час я планую написати про те, в чому дещо знаю: опуклі множини, операції з ними, оптимізацію та теорію ігор. Тут багато можливих тем.
30 Липня 2019, 12:37
Круто, круто, круто!
30 Липня 2019, 20:15
я думаю, що основи пояснити може будь-який математик)
30 Липня 2019, 15:03
Прекрасна стаття! Із задоволенням прочитаю продовження 🙂
31 Липня 2019, 07:28
Сподобалося
31 Липня 2019, 22:53
Дякую, цікаво! Тільки кватерніони, здається, не утворюють поле. Там немає комутативності.
31 Липня 2019, 23:44
Так, моя помилка, там кільце кватерніонів.
Напишіть відгук