Розкладай та володарюй. Математичні ряди та мистецтво нехтування

Трансценде́нтні чи́сла

Думаю, не буде перебільшенням сказати, що розвиток математики в давні часи був тісно пов’язаний з визначенням периметрів і площ різних ділянок землі¹. Стародавні математики вміли визначати площі квадратів, прямокутників, трикутників, трапецій, ромбів тощо – плоских фігур, за допомогою яких описували ці ділянки. Ці навички пов’язані з оперуванням числами, що можна виразити через відношення цілих – тобто за допомогою раціона́льних чи́сел. (Про те, які бувають числа, читайте тут). Однак є така фігура, про яку напевно знали найдавніші цивілізації, однак не могли визначити через відношення ані її периметру, ані площі. Це – круг². У круга є ра́діус (відстань від центра до країв) чи діа́метр (удвічі більше), але довжину кола та площу неможливо виразити через них за допомогою будь-яких відношень. Звісно, можна виміряти довжину кола та діаметр і поділити одне на інше. Це відношення називають числом π.

Як можна виміряти число π. Автор: John Reid – Edited version of Image:Pi-unrolled.gif., CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=1268581

Однак це не буде математичним визначенням! Ми знаємо, що будь-які вимірювання мають свої похибки.

Коло – не єдина “дивна” фігура. Можна ще звернути увагу на питання про довжини всіх сторін прямокутного трикутника. Звичайно, є так званий єгипетський трикутник, який має прямий кут, а довжини сторін мають відношення, як цілі числа 3:4:5. Але він є радше винятком, ніж  правилом. Найчастіше все ж таки не вдається виразити більшу сторону (гіпотену́зу) через дві менші (ка́тети) використовуючи тільки чотири арифметичні операції (додавання, віднімання, множення, ділення).

Приклад прямокутного трикутника. Кут при вершині C є прямим, сторони a та b є катетами, а сторона c є гіпотенузою. Якщо нам відомі довжини катетів, тоді довжину гіпотенузи можна обчислити як корінь з суми квадратів катетів . Це випливає з Теореми Піфагора. Джерелом зображення є сторінка вікіпедії: CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=617373   

Та все одно з довжинами гіпотенуз ситуація суттєво легша. Хоч більшість квадратних коренів і належить до ірраціона́льних чи́сел, ми все ж можемо математично визначити ці числа через раціона́льні. Вони належать до більшої множини алгебраї́чних чи́сел³, які можна виразити через раціональні за допомогою алгебраїчних рівнянь з многочле́нами.

Приклад прямокутного трикутника, довжина гіпотену́зи якого дорівнює корінь квадратний з двох – ірраціона́льному числу. Автор: derivative work: Pbroks13 (talk)Square root of 2 triangle.png: en:User:FredrikSimplified drawing: Rubber Duck (☮ • ✍) – Square root of 2 triangle.png, Суспільне надбання (Public Domain), https://commons.wikimedia.org/w/index.php?curid=4322869

З колом  ситуація набагато цікавіша, оскільки відношення довжини кола до діаметру є не алгебраїчним числом, а трансценде́нтним. Скільки не намагайся, годі виразити його через рівняння з раціональними числами⁴. Якщо ви думаєте, що таких чисел небагато, ви помиляєтеся. Насправді, множина трансцендентних чисел є не тільки нескінченною, але й незліче́нною (у своїй статті про числа я пояснював, що це значить). 

То як же нам визначити, скільки то є – π? Ще Архіме́д намагався робити оцінки згори на знизу, обчислюючи периметри опи́саних та впи́саних в коло правильних багатокутників:

Приклади вписаних в коло та описаних навколо нього правильних багатокутників, обчисливши периметри яких можна оцінити число π з гори та знизу. Автор: !Original: FredrikVector: Leszek Krupinski – Власний твір заснований на: Archimedes pi.png:  від Fredrik., Суспільне надбання (Public Domain), https://commons.wikimedia.org/w/index.php?curid=1250248

Що більше сторін в багатокутників, то точнішими будуть оцінки. Взявши 96-кутники античний мислитель визначив, що π більше ніж 3 + 10/71 та менше ніж 3+1/7. Якщо перевести ці значення в десяткові дроби, то можна побачити, що два знака після коми – 3.14 – він відтворив. Небагато,  але цієї точності, напевно, вистачало тодішнім інженерам.

Послідовніть. Границя.

Оцінка числа π, описана вище, хоч і може поліпшуватися (за рахунок збільшення кількості сторін у багатокутників), але точною ніколи не буде. Для того, щоб зробити наступний крок до математичного визначення, скільки то є – π, нам знадобиться поняття послідо́вності. Розглянемо периметри багатокутників, скажімо, впи́саних в коло діа́метру 1, як річ залежну від кількості сторін. Остання може бути будь-яким натуральним числом, відповідно ми отримуємо пронумерований нескінченний (але зліченний) ланцюжок периметрів (дійсні числа). Саме така річ і називається послідовністю. У прикладі з тим, що робив Архімед, можна побудувати другу послідовність – периметри опи́саних навколо круга багатокутників.

Деякі послідовності (в тому числі, дві описаних вище) мають грани́цю⁵. Наскільки би маленький о́кіл біля неї ми не обрали, знайдеться такий номер, що починаючи з нього всі елементи послідовності опиняться в цьому о́колі. Про послідовність з границею кажуть, що вона пряму́є (або пра́гне) до цього значення. Питання про те, як довести факт існування в конкретної послідовності границі і встановити її значення, я залишу найбільш зацікавленим на самостійне ознайомлення. А решту запевняю, що ці методи вже давно опрацьовані математиками і знайшли багато застосувань у різних науках.

То ж послідовність периметрів вписаних багатокутників буде прямувати до π знизу (Кожний з них є менший за π, але ближчий до нього ніж попередні). А периметри описаних багатокутників прямуватимуть до π згори.

Такий приклад послідовностей є ілюстративним, бо дозволяє оцінити те, що ми не можемо визначити через звичайні рівняння. Однак він не дуже зручний, бо нам важко написати формулу за якою можна було би порахувати будь-який елемент, знаючи його номер. В якості більш простого прикладу послідовності, що має границю, можна запропонувати, наприклад, таку: a_n=1/n. Тут літера a – це назва послідовності, a_n – це її елемент під номером n. Права частина рівняння – це, власне, формула, за якою можна визначити елемент під будь-яким номером n. Границею цієї послідовності є число 0: ми можемо обрати як завгодно малий інтервал навколо нуля, і завжди знайдеться таке n, починаючи з якого всі числа 1/k(k>n) потрапляють в нього. Кожний наступний елемент цієї послідовності менший за попередній, тобто вона моното́нно спадає. Якщо ми змусимо нашу послідовність, наприклад, чергувати знак (a_n=±1/n), вона все одно прямуватиме до нуля, але вже не моното́нно.

Окрім границь послідовностей бувають також границі функцій визначених на дійсних та навіть на комплексних аргументах. Разом вони дають математикам дуже потужний інструмент, що є основою математи́чного ана́лізу. (Про важливість граничного переходу в математиці я вже згадував).

Ряди та нехтування

Є такий цікавий тип послідовностей, якому дали спеціальну назву. Це послідовність сум, така, що кожна наступна сума містить на один додаток більше, ніж попередня. Її називають послідовністю часткових сум, а послідовність додатків, що додаються, називають ря́дом. Якщо послідовність часткових сум має границю, то вона називається сумою ряду. Ряд, в якого є сума, називається збі́жним. Коли ж послідовність часткових сум не має границі, тоді ряд є розбі́жним. 

Анекдот про суму ряду: 
Заходить у бар нескінченна (але зліченна) кількість математиків. 
Замовляють по черзі:
- Бокал пива, будь ласка.
- Половину пива.
- Чверть.
- Одну восьму. 
Бармен зупиняє: 
- Знаю я ваші фокуси. Ось вам ваші два бокали пива. Хто платитиме?
- Той, хто стоїть точно посередині!

Замість обчислення периметрів багатокутників є легші способи визначити й оцінити число π. Наприклад, як суму ось такого ряду⁶:

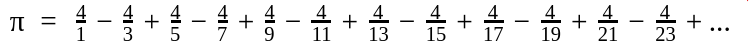
Це буде водночас і математично точне визначення, бо значення суми ряду існує і воно має певне значення. Також це спосіб оцінити цю суму з потрібною точністю. Існують методи, як визначити похибку оцінки суми ряду за частковою сумою, однак вони занадто складні для цієї статті.

Є ще одне відоме трансцендентне число – e. Цікава властивість цього числа, що похідна́ функції e^x дорівнює такій самій функції, робить його дуже важливим в математичному аналізі. Його теж можна визначити через суму ряду (але іншого, звісно):

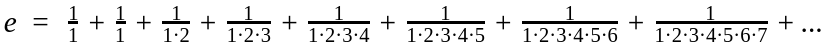
Коли є величина, яку ми хочемо оцінити, як суму ряду⁷, але не маємо самого ряду, то задача знайти його називається розкла́сти цю величину в ряд. Загального рецепту для цього не існує, але є типи рядів, які підходять для деяких ситуацій. Коли, наприклад, ми не можемо обчислити точне значення якоїсь непере́рвної та гладко́ї функції в довільній точці, але знаємо її похідні́ в іншій, нам підходить ряд Те́йлора. А періодичні неперервні функції можна розкладати в ряд Фур’є́, що дозволяє, на приклад, описати звучання струни з урахуванням усіх вищих гармонік (їх ще називають обертонами).

Дуже багато практичних задач з наближеного обчислення зводяться до розкладу функцій у той чи інший ряд. Вони широко використовуються в багатьох науках. У теоретичній фізиці, наприклад, є такі задачі, які не мають аналіти́чного ро́зв’язку (коли відповідь можна записати у вигляді формули і порахувати). Простим і яскравим прикладом є задача руху трьох чи більше тіл, що попарно взаємодіють силами гравітації. Загального точного рішення вона не має, хоча можна вдатися до хитрощів. Ось, наприклад, у Сонячній системі є багато планет та супутників, але Сонце настільки масивне, що його вплив на рух планет є визначальним. Тому для обчислення руху якоїсь планети можна спочатку порахувати, як вона оберталася би, якби окрім Сонця більш нічого не було. Потім можна по черзі врахувати вплив на орбіту потрібної планети всіх інших, якщо мати певні припущення щодо їхнього руху. Можна так само порахувати, як вони оберталися би навколо Сонця, якби були самотні. Якщо потрібна краща точність, то можна таким порахувати “уточнені” орбіти для всіх планет і повторювати процедуру скільки завгодно. Такий підхід до розв’язку задач руху багатьох тіл називається тео́рією збу́рень.

Окрім нього існує ще адіабати́чне набли́ження, яке застосовують коли всі взаємодії є достатньо сильними, однак реакція однієї частини системи на інші зміни є дуже швидкою. На приклад авто має ресори, що деформуються під вагою кузова (й тих, хто всередині). Якщо їхати ідеально рівною дорогою, то вага і деформація ресори не змінюються. Якщо починається пологий спуск, то вага авто трошки зменшується при проїзді через викривлення дороги на початку. В кінці спуску – теж через викривлення – вона на якийсь час збільшиться. На підйомі буде навпаки. Деформація ресори теж буде змінюватися разом з вагою. Якщо все це відбувається достатньо повільно, то можна вважати що ресора завжди “підлаштована” під вагу. Такий опис і є адіабатичним наближенням⁸. Однак якщо авто наїде на яму, тоді зміни будуть занадто швидкими. Підвіска почне коливатися. Коли яма не надто глибока, а авто не надто швидко їде, амортизатори погасять коливання, які можна вважати збуренням руху авто. Коли ж яма велика, і авто наїжджає швидко, стається аварія – жодне з наближень не виправдане.

Розклад функцій в ряди дозволяє не тільки наближено обчислити те, що не має точного розв’язку. Це також інструмент для встановлення меж застосування старих теорій, коли після нових відкриттів з’являються нові – більш загальні, але складніші. (Про самовдосконалення науки можна прочитати тут). Серед фізиків є жарт, що фізика є наукою про те, чим і коли варто знехтувати. Це дуже близько до правди, і саме математичні ряди дають кількісні критерії, коли нехтувати доречно.

Примітки

1. Навіть назва дисципліни геоме́трія походить з грецької мови і перекладається як “вимірювання землі”.
2. Колом називається крива, що складається з точок рівновіддалених від центру. Круг – ділянка площини, обмежена колом. Отже коректно говорити про довжину кола, та про площу круга (не переплутайте).
3. На сторінці Вікіпедії множину алгебраїчних чисел визначено як підмножину комплексних чисел. Це правильно, але в цьому тексті можна обмежитися дійсними алгебраїчними числами. На приклад корені рівняння x²=-2 не підходять, бо не є дійсними числами, а от корені рівняння x²=2 – підходять, бо це корінь з двох та мінус корінь з двох.
4. Через інші неалгебраїчні – дуже легко. На приклад є ось таке коротеньке рівняння, яке, правда, вимагає нас працювати в множині комплексних чисел: e^iπ=-1. Але нам також потрібно знати число e, яке теж не є алгебраїчним.
5. На сторінці Вікіпедії визначення звучить так складно, тому що там розглядають більш загальне поняття послідовності. Нам тут достатньо обмежитись тими послідовностями, елементами котрих є дійсні числа (взагалі, можуть бути й інші речі, наприклад, вектори). Границя тоді, якщо вона існує, теж буде дійсним числом.
6. Є також багато інших способів визначити число π, як нескінченну суму. Є кращі, ніж ця сума тим, що сходяться швидше (для такої самої точності оцінки достатньо меншої кількості додатків ряду). Однак саме ця сума є достатньо простою, щоб навести її тут.
7. Вище в тексті йшлося про послідовності (і ряди), елементами котрих є числа. Однак, ними можуть бути також функції. Тоді і сумою збіжного ряду буде функція.
8. Тут наведено приклади з класичної механіки, однак не менш плідним цей підхід є у фізиці мікросвіту (де все описує квантова механіка). Теорія збурень дуже часто використовується в атомній фізиці. В атомі електрони розташовуються на орбіталях навколо атомного ядра, що є центром. То ж їхні властивості розраховуються з урахуванням взаємодії один електрон – ядро, а потім враховують ефекти спричинені взаємодією з зовнішнім чинником. Яскравими прикладами є ефекти пов’язані з розщепленням станів атома в магнітному та електричному полях. (Взаємодію атомних електронів між собою враховує при́нцип Па́улі). Адіабатичне наближення дуже широко використовують для опису взаємодії молекул: коли вплив однієї молекули на іншу змінюється повільніше, ніж кожна всередині підлаштовується під зовнішні зміни.

Джерелом титульного зображення є сайт pixabay.com

Повний список моїх математичних статей:

• Числа (цілі, раціональні, дійсні, комплексні)
• Математичний простір. Скаляри та вектори
• Імовірності. Розподіли. Статистика. Похибка
• Трансцендентні числа. Математичні ряди. Наближені обчислення
• Послідовності. Прогрессії. Відсоткова ставка кредитів