Простір у математиці

Математика часто дивує нас тим, що поняття, впроваджені для одних цілей, дивовижним чином знаходять застосування в інших галузях. Про́стір є одним з них: з’явившись у геометрії, він проник майже в усі розділи математики, а через неї — у фізику, хімію, економіку, соціологію та інші науки.

Почнемо наше вивчення простору саме з геометрії. Якщо сказати просто, то це такий спосіб описати можливі відносні розташування об’єктів. Простір складається з ве́кторів, кожен з яких має числове значення (яке називають мо́дулем або довжино́ю) та напрямок. Вектор показує наскільки один об’єкт далеко знаходиться від іншого та з якої сторони розташований. Існує нескінченна кількість векторів. Ба більше, простір — їх множина — є незліченним (У статті про числа я вже пояснював значення цього терміну).

З векторами можна виконувати деякі арифметичні операції, як із числами.

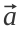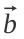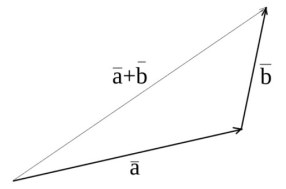
• Існує додавання векторів: нехай від мене на певній відстані у певну сторону знаходиться дерево (це можна представити вектором ), а від цього дерева відомо напрямок і відстань до білого гриба у траві (вектор ) — через додавання цих двох векторів ми дізнаємося відстань і напрямок, де знаходиться цей гриб відносно мене ().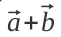
  
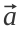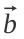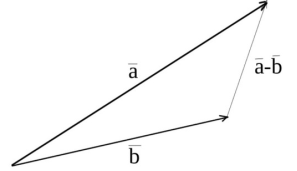
• Як обернену операцію можна впровадити віднімання: я бачу гриб () біля дерева () і хочу дізнатися, як розташований цей гриб відносно дерева ().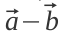
  
• Вектор можна помножити на дійсне число: якщо я маю напрямок і відстань до дерева, я можу визначити, що таке удвічі чи утричі далі (помножити вектор на 2 чи 3 відповідно), або ж удвічі чи утричі ближче (на 1/2 чи 1/3 відповідно). Можна також множити вектор на від’ємне число (отримуємо протилежний напрямок).

Як серед чисел є нуль, так само існує нульовий вектор, що є представленням положення об’єкту відносно самого себе. Його й тільки його модуль дорівнює нулю.

У формулах вектори, зазвичай, позначують стрілочкою вгорі, але бувають і інші способи (рисочка, виділення жирним шрифтом тощо). Операції над векторами мають такі властивості:

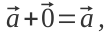
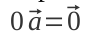• — властивості нульового вектора
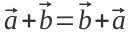• — можливість переставляти доданки у сумі векторів
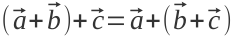• — можливість змінювати порядок послідовних додавань
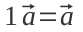• — множення вектора на одиницю не змінює його
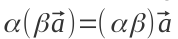• — помножити вектор на одне число, а потім на друге — те саме, що помножити на їхній добуток
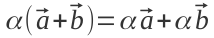• — добуток суми векторів на число — те саме, що сума добутків
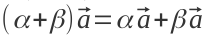• — так само для добутку суми чисел і вектора

Властивості цих операцій пов’язані з властивостями простору. В математиці його називають ліні́йним або ве́кторним про́стором¹.

Базис. Координати вектора. Метрика

Коли ми впроваджуємо напрямок вектора, то показати рукою зі словами “от туди” нам напевно не вистачить для досягнення математичної точності. Однак для того, щоб описати напрямки кількісно, треба вдаватися до певних хитрощів.

Якщо два вектори мають один і той самий напрямок, тоді можна знайти таке число, що помноживши на нього один вектор отримаємо другий: . Якщо треба множити на від’ємне число, то вектори мають протилежний напрямок, але лежать на одній прямій. Такі вектори називають ліні́йно зале́жними.

Однак, на площині є безліч способів знайти два вектори, що не лежать на одній прямій. Для кожної такої пари не існує числа, щоб помноживши на нього один вектор вдалося отримати другий (такі вектори називаються ліні́йно незале́жними). Вибравши довільним чином пару таких векторів та , всі інші вектори на площині можна представити у вигляді такої суми: , при чому для кожного вектора пара чисел x та y є тільки одна, та вона однозначно ідентифікує цей вектор.

Обрані вектори та називаються ба́зисом, а числа x та y — компоне́нтами вектора в цьому базисі. Коли ми додаємо вектори, то їхні компоненти додаються, коли віднімаємо — віднімаються. Множення вектора на число є множенням всіх його компонентів на це число.

На площині базисом може бути будь-яка пара векторів, що не лежать на одній прямій. Якщо вектори базису та перпендикуля́рні, а їхні модулі дорівнюють одиниці, тоді він називається ортонормо́ваним ба́зисом. У ньому легко визначити модуль будь-якого вектора, маючи його компоненти: (теорема Піфагора відповість на питання, чому саме так).

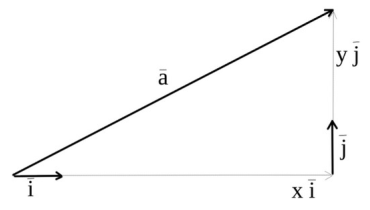
Для того, щоб впровадити абсолютні координати точок на площині, окрім базису треба обрати ще опорну точку (поча́ток координа́т), відносно якої визначатимуться положення всіх інших точок на площині. Компоненти вектора, що описує положення довільної точки відносно опорної, можна вважати її координатами. Обравши собі на площині ортонормований базис і початок координат, отримаємо відому нам зі школи дека́ртову систе́му координа́т.

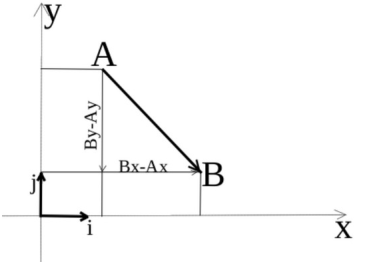
Маючи координати двох точок в такій системі, можна обчислити відстань між ними: Правило визначення відстані між точками називається ме́трикою. Метрику, задану за теоремою Піфагора, називають евклі́довою.

На площині базис будується з двох векторів, тому вона є двови́мірним простором. Об’ємні фігури можна описати в іншому просторі, що має не два, а три ви́міри. Це значить, що маючи два лінійно незалежні вектори, можна знайти (у безліч способів) ще один, який не можна представити через ці два відомими нам операціями додавання та множення на число. Отже можна знайти вже не два, а три лінійно незалежні вектори. Такої трійки векторів буде достатньо, щоб описати всі інші вектори простору: Так само, обравши базис перпендикулярних векторів одиничної довжини, ми знайдемо довжину будь-якого вектора за його компонентами: Так само, обравши опорну точку в просторі, можна отримати тривимірну декартову систему координат. Тільки в ній буде вже не дві, а три вісі. Тривимірний простір, що ми отримали, називається евклі́дів про́стір. В ньому кожна точка має три координати, а відстань між точками визначається за евклідовою метрикою:

Можна узагальнювати далі і побудувати чотиривимірний евклідів простір, п’ятивимірний і так далі. Кількість векторів у базисі буде дорівнювати кількості вимірів. В математиці також використовуються простори з іншими метриками, наприклад метрика Мінковського, яка знайшла застосування в теорії відносності.

Числовий запис вектора Коли ми вибрали базис, то будь-який вектор у просторі можна представити як впорядковану комбінацію чисел (його компонент). Впорядкованість означає, що не можна плутати різні координати. У формулах зазвичай для позначення компонент використовують нижній індекс: де – вектори базису. 

Перетворення базису.

Уявімо собі ситуацію, коли ми спочатку обрали собі якийсь базис і знайшли представлення потрібних нам векторів у ньому. Але потім сталося так, що цей базис перестав нас влаштовувати, і ми обрали інший. Що тоді робити з представленням векторів?

Спочатку, звісно, треба уникнути плутанини з позначеннями. Давайте вектори старого базису назвемо а нового — . Кожний вектор простору можна представити як в одному базисі так і в іншому . Компоненти вектора залежать від того, в якому базисі ми його представляємо.

І тут у математиків виникає така задача: нехай ми знаємо, як вектор представлено в старому базисі, а нам треба дізнатися, які будуть його компоненти в новому базисі. Що для цього треба? Як це зробити? Чи можливо це зробити з будь-яким вектором?

Для цього треба мати представлення векторів старого базису в новому:

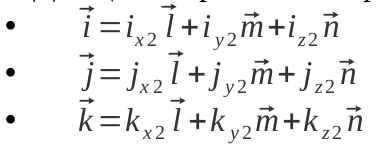
Тепер маючи визначення вектора в старому базисі можна підставити туди представлення старих базисних векторів у новому базисі. Ми отримаємо досить громіздкий вираз:

== . ²

Його можна спростити, згрупувавши ці додатки по векторах вже нового базису: = .²

Три частини виразу в дужках є нічим іншим, як компонентами вектора в новому базисі:

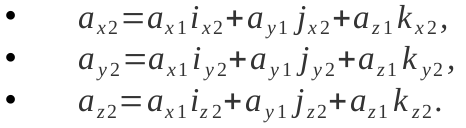
Представлення будь-якого вектора можна перевести з одного базису до іншого, маючи представлення векторів старого базису в новому. Прошу звернути увагу, що в останніх трьох виразах присутні лише числа. Від простору і векторів, які описують взаємне розташування об’єктів (геометрії), ми перейшли до рівнянь з числами (алгебри), що описують ті самі речі.

Щоб не записувати громіздких виразів, можна скористатися спрощеним записом:

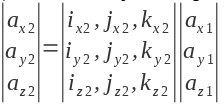
На вектор, представлений у старому базисі, записаний у вигляді стовпчика, ми діємо ма́трицею перетво́рення (її елементи ми впізнаємо — вони з формул вище) і отримуємо представлення цього вектора в новому базисі. З тим, як визначене мно́ження ма́триць, яке тут використовується, зацікавленим пропоную ознайомитися самостійно.

Розділ математики, що оперує матрицями називається ліні́йна а́лгебра. Там вектори записуються числами (компонентами) в рядок або у стовпчик. Але мати такий запис недостатньо. Щоб числа записані у стовпчик чи в рядок були вектором, потрібне ще правило їхнього перетворення при заміні базису. Воно для всіх векторів простору однакове.

Скалярний добуток. Скаляр.

Якщо ми обмежимо свій вибір базису в просторі лише ортонормованими тоді ми можемо ввести ще одну цікаву операцію — скаля́рний до́буток двох векторів. У тривимірному просторі його визначають так:

Така операція має властивості дуже схожі на множення чисел:

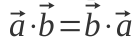• — можна переставляти вектори місцями
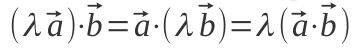• — помножити один з векторів на число — це те саме, що помножити весь добуток на це число.

Зверніть увагу на ще одну цікаву річ: в якому ортонормованому базисі ми би не представили вектори, їхній скалярний добуток, визначений у такий спосіб, має завжди однакове значення. Саме тому в його назві використовують слово “скаля́рний”. Воно означає, що величина описується числом, яке залежить від векторів але не залежить від базису, в якому їх представлено. Математики називають це інваріа́нтністю відносно перетворень базису.

Якщо взяти скалярний добуток вектора самого на себе, то ми отримаємо: А це є ніщо інше, як квадрат його довжини (модуля). Отже метрика теж є інваріантною відносно перетворення базису³. Навіть коли ми маємо справу з іншими метриками, вони теж обов’язково зберігають цю властивість.

Скалярний добуток має безліч використань. У фізиці, наприклад, він фігурує і у визначенні роботи та енергії, і в описі руху похилою площиною чи криволінійною траєкторією, і в електродинаміці, і в багатьох інших сферах. Окрім цього є багато інших скалярів, найвідомішими з яких, мабуть, є енергія та маса.

Окрім векторів та скалярів у просторі можна визначити ще псевдовектори та псевдоскаляри. Судячи з назви, це речі, які виглядають як звичайні вектор та скаляр, але ними не є. Відрізняються вони тим, що не зберігають інваріантності при деяких перетвореннях базису. Якщо вам цікаво, і ви напишете про свою зацікавленість в коментарях, у наступній статті я розкажу вам, де у фізиці зустрічаються ці дивні математичні об’єкти.

Примітки

1. Часто визначають також операції множення векторів: скалярного та векторного, але для того, щоб мати лінійний простір, достатньо лише наведених у тексті.
2. Можливі перетворення виразів з векторами визначаються властивостями, наведеними у першій частині цього тексту.
3. У базисі, що не є ортонормованим, метрика теж зберігається, але щоб урахувати таку можливість, потрібно записати її складнішою формулою.

Джерело титульного зображення: pixabay.com

Повний список моїх математичних статей:

• Числа (цілі, раціональні, дійсні, комплексні)
• Математичний простір. Скаляри та вектори
• Імовірності. Розподіли. Статистика. Похибка
• Трансцендентні числа. Математичні ряди. Наближені обчислення
• Послідовності. Прогрессії. Відсоткова ставка кредитів