Система небесних координат

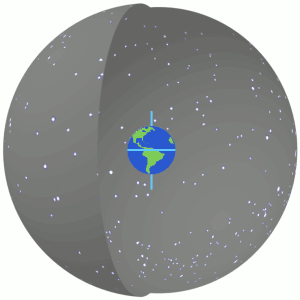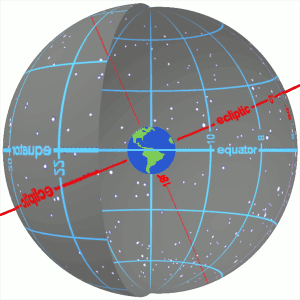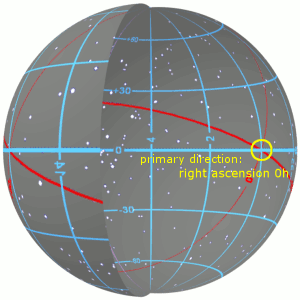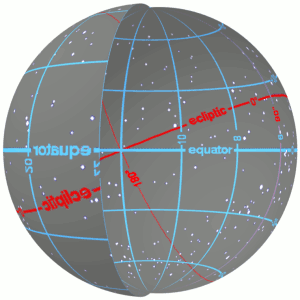
Система координат — це найточніший спосіб визначити взаємне положення двох чи більше точок на площині чи у просторі. У астрономії застосовується кілька систем координат, однак усі вони є сферичними, тобто описують небо як сферу. Є основна площина, яка перетинає цю сферу, утворюючи коло. Є пряма, перпендикулярна цій площині, що утворює два полюси.

У якості прикладу можна узяти екваторіальну систему координат. У неї основною площиною є та, що проходить через небесний екватор, а північний полюс співпадає із напрямком на Полярну зорю. Перша координата називається схиленням і являє собою кут між напрямком на небесний екватор та напрямком на об’єкт. Вимірюється у градусах і може бути від -90 до 90. При цьому -90 — напрямок на південний полюс, 0 — на екватор, 90 — на північний полюс. Друга координата називається прямим піднесенням і вона являє собою кут між небесним меридіаном весняного рівнодення та небесним меридіаном, на якому знаходиться зоря. Однак на відміну від схилення, пряме піднесення вимірюється у годинах, хвилинах і секундах.

Така система координат може здатися досить дивною, однак для наземних спостережень вона була і ще довго буде залишатися основною. Бо небо над нашою головою змінюється в залежності від часу доби, пори року і положення спостерігача на земній кулі. Однак як би не змінювалося небо, кути між зірками завжди залишаються одними і тими ж самими і застосовуючи систему кутів легко можна робити перерахунки, визначаючи час і місце появи тієї чи іншої зорі у для конкретної точки спостереження досить неважко. Саме ця система дозволяє надійно ідентифікувати об’єкти у небі.

Проблема полягає у тому, що наш всесвіт не є вогниками на темній сфері, а являє собою величезну тривимірну структуру. І якщо ми спробуємо достатньо точно хоча б невелику частину цієї структури собі уявити користуючись екваторіальною системою координат, то дуже швидко зрозуміємо, наскільки це важко. По перше до двох координат доведеться додати ще третю — відстань до об’єкту. По-друге, розуміння положення зірок це не дуже полегшує. Наприклад розглянемо досить просту задачу. У нас є три зірки із відомими прямими піднесеннями, схиленнями та відстанями до них. Треба визначити відстані між цими трьома зірками. Рішення такої задачі у сферичних координатах настільки складне із застосуванням тригонометричних функцій, що зазвичай її вирішують, просто переходячи до координат декартових, у яких вона вирішується за формулою D=sqrt((x2-x1)^2+(y2-y1)^2+(z2-z1)^2). Тобто усе що треба — це прямокутна система координат XYZ, знайома мабуть усім. Значно простіша у використанні і більш інтуїтивно зрозуміла, ніж сферична, однак абсолютно непридатна для ведення спостережень із Землі. У обсерваторіях нею користуватися абсолютно неможливо.

Однак користуватися екваторіальною системою координат добре, коли ти сидиш біля її початку і нікуди не рухаєшся. Коли ж ти починаєш пересуватися простором, який цією системою координат описується, о швидко розумієш, яка вона незручна. Спробуйте поїздити Харковом, користуючись у якості координат азимутом на ваше місцезнаходження, узятим від Держпрома та відстанню до нього. Причому враховуйте, що їхати вам треба не до Держпрома, а, наприклад з Холодної Гори на Основу, причому найкоротшим шляхом. А тут воно ще у тривимірному просторі. І “азимутів” аж два штуки одночасно.

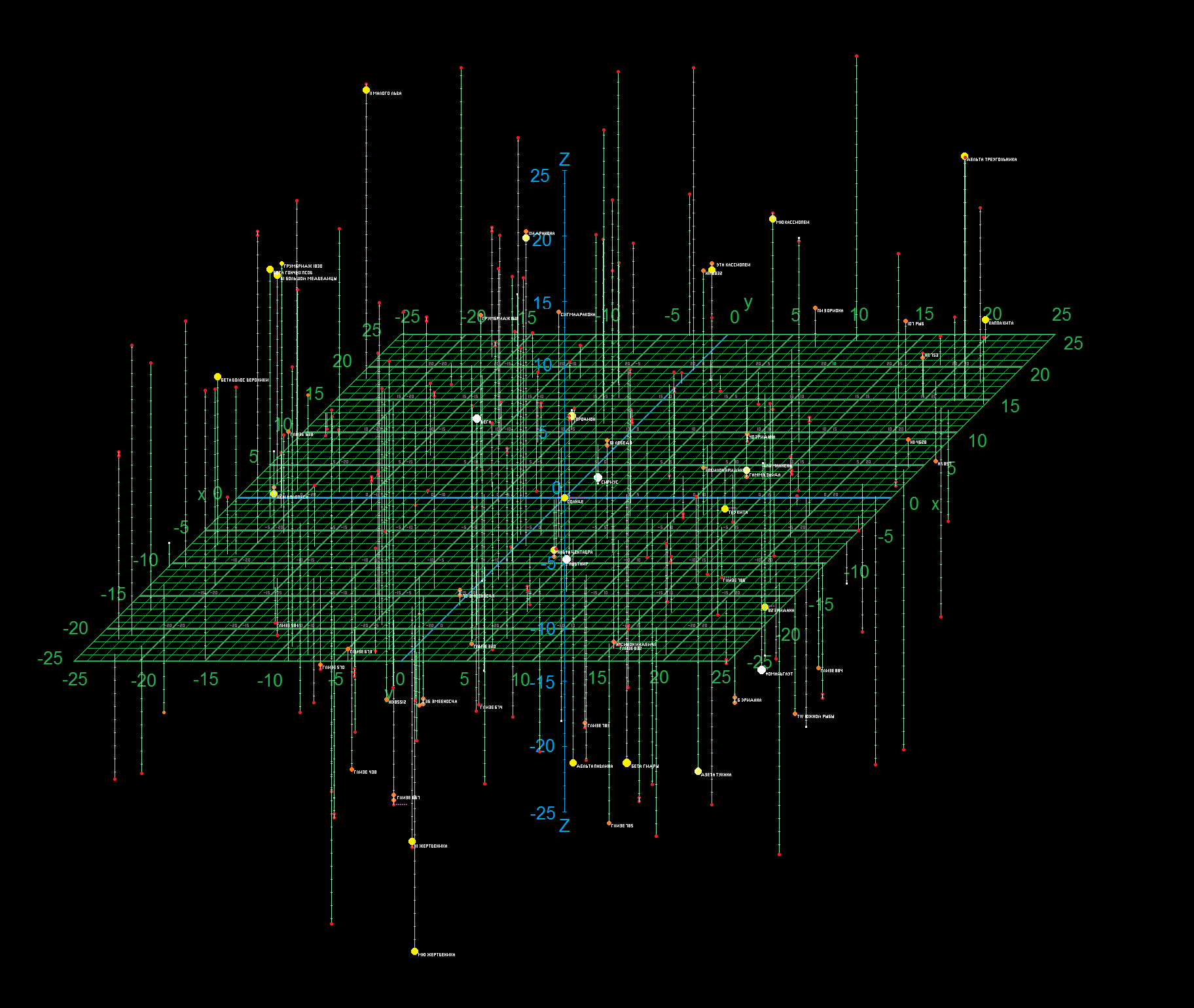
Тому можна припустити, що у майбутньому, коли людство навчиться пересуватися між зорями основною буде саме декартова система координат, якою б невдалою для сучасних спостерігачів вона не була.