Що таке теорія відносності? Частина 2. Простір і час.

З першої частини ми дізналися, як просте питання про швидкість світла змусило фізиків переглянути свої уявлення про світ.
Цього разу ми дещо зануримося у світ математики, щоб дізнатися про джерело нових уявлень.

До першої частини

Що таке простір?

Простір — це математичний спосіб опису розташування об’єктів.

Зі школи ми знаємо, що положення на площині можна представити в Декартових координатах. В тривимірному просторі можна робити так само, тільки з’являється ще третя вісь, а отже положення описується трьома координатами. Але чи наявності трьох осей достатньо, щоб говорити про простір?

Виявляється, що ні. Нам ще потрібна метрика — це те, в який спосіб ми визначаємо відстань між двома точками, маючи їхні координати. В школі на математиці ми робили це за теоремою піфагора:

Коли є третій вимір, в цій формулі з’являється ще третій додаток. Метрика є важливою характеристикою простору, але не вичерпною. Поставимо просте запитання: якщо ми декартові вісі пересунемо, чи матимемо інший простір? Ні, простір матимемо той самий, але отримаємо іншу систему координат в ньому. Правила перетворення координат при пересуванні осей теж є властивістю простору. Цього, на данний момент, нам буде досить.

Слід зауважити, що відстані між точками у просторі не залежать від системи координат, в якій ми його представляємо, або, як кажуть математики, метрика простору є інваріантною відносно перетворення координат.

Простір в класичній фізиці

В класичній фізиці використовується евклідовий простір, який ми вивчали в школі на уроках геометрії, хоча нам не казали, що то був саме він. Геометрія на площині — планіметрія — працює з двовимірним евклідовим простором, а стереометрія — з тривимірним.

В Ньютонівській механіці, як ви мабуть вже здогадалися, використовується тривимірний простір. Хоча в деяких задачах опис положення тіл можна спростити до двох- чи навіть одновимірного випадку. На приклад, коли ми хочемо описати вагони на колії, то бажання виключити два з трьох вимірів, пустивши єдину вісь вздовж рейок, є цілком виправданим.

Час в класичній фізиці

А яка ж ситуація з часом у фізиці? Час ми визначаємо теж відносно якоїсь події. На приклад, годинник, якщо йде правильно, показує скільки часу минуло з останньої опівночі. Календар дозволяє рахувати дні з першого січня, хоча також групує ці дні по місяцях. Роки ми рахуємо від початку нашої ери, тобто коли давні люди домовилися рахувати роки в той спосіб, що зберігся дотепер. Отже можна говорити про “часову координату”, яка визначається від певного “початкового” моменту. Є в часу також метрика, адже ми визначаємо довжину часових проміжків. Є також правила перетворення цієї координати. Якщо ми переїдемо до іншого часового поясу, то ми, або наші ґаджети, будуть виконувати як раз таке перетворення. При цьому довжина проміжку часу буде такою самою незалежно від поясу. Узагальнюючи можна сказати, що звичний нам опис часу цілком ідентичний одновимірному евклідовому простору.

В Ньютонівській фізиці простір і час є незалежними один від одного в тому сенсі, що в усіх точках простору час плине однаково, та в усі моменти часу властивості простору однакові.

Математична забавка стала в нагоді

Така несподіванка, що світло рухається з однаковою швидкістю в усіх інерційних системах відліку, поламала нам всі уявлення про час і простір. Теоретикам, щоб описати всесвіт з урахуванням цього, знадобилася якась альтернатива евклідовій геометрії.

І вона знайшлася, бо математики тоді вже встигли вигадати простори з альтернативними метриками та правилами перетворення координат. Ці забавки на той час не мали застосування, та, на щастя, попри це науковцям ніхто не заважав. Серед того різноманіття “альтернативних геометрій” Ейнштейн знайшов математичний простір, який підійшов для цієї задачі. Давайте подивимось, що він зробив.

Спочатку треба об’єднати простір і час в один чотиривимірний простір-час. В ньому кожна подія має чотири координати — одну часову і три просторових.

Якщо замість відстані взяти іншу метрику — метрику Мінковського

,
то для забезпечення її незмінності доведеться змінити також правило перетворення координат на правила Лоренца. Якщо використовувати такий простір у механіці, то можна описати цікаві ефекти.

Одночасність — відносна

Як так може бути? Уявімо собі вагон, який їде з постійною швидкістю, отже є інерційною системою відліку. Посередині вагона розташоване джерело світла (0), а в кінцях, на рівній відстані від нього — спостерігачі (1 та 2). Джерело спалахує — світло досягає спостерігачів.

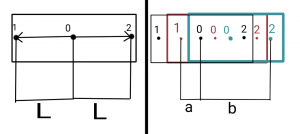
Якщо ми опишемо ситуацію відносно вагона (ліва половина малюнку), то світло подолає однакові шляхи до обох спостерігачів, а отже досягне їх одночасно. Відносно нерухомої платформи (права половина малюнку) світло рухається з такою самою швидкістю, а отже подолає різні шляхи, бо всі три учасники рухаються разом із вагоном. Відповідно, світло досягне спостерігачів не одночасно.

Катастрофа? Знов, ні!

Здавалося б, відносність одночасності повинна зламати також наші уявлення про причинно-наслідкові зв’язки між подіями. Припустимо, що в одній системі відліку ми встановили, що подія A є причиною B. Якщо в іншій системі відліку B відбудеться раніше за A то буде якась нісенітниця — наслідок передує причині. Чи може причинність теж відносна?!

Виявляється, якщо з теорії виключити можливість руху швидше за світло, чого дійсно ніколи не спостерігалося, тоді все стає на свої місця. Одна подія може бути причиною іншої, якщо від неї може дійти якийсь сигнал, чи щось долетіти. А долетіти може — не швидше за світло.

На малюнку наведено спрощене зображення координат простору-часу. В початку координат (“тут і зараз”) знаходиться подія A. Сині конуси показують, як може рухатися світло, яке ми “тут і зараз” бачимо (нижній), або яке випромінюється “тут і зараз” (верхній). Подія B знаходиться всередині верхнього конусу, отже вона може бути спричинена подією A. Події всередині нижнього конусу можуть бути причинами події A. Подія C знаходиться поза конусами. Це її одночасність, чи неодночасність з A є відносною. А щодо події B — вагони не можуть їхати швидше за світло.

Що ж значить така дивна метрика?

Настав час відповісти на питання, що ж значить метрика Мінковського. Якщо одну подію зафіксувати на “тут і зараз”, і рахувати “відстань Мінковського” між нею та усіма іншими подіями часу-простору, то її сенс буде очевидним. “Відстань” до усіх подій на обох світлових конусах буде рівна нулю, для подій всередині конусів вона буде додатньою, а для подій поза конусами — від’ємною. Як належить кожній метриці, метрика Мінковського не змінюється при переході в іншу систему відліку.

Таким чином ми маємо точний критерій, коли можливий причинний зв’язок між подіями, а коли — ні.
Космос — це цікаво, а яка користь на Землі?

• В прискорювачах частинок, а це не тільки наукові об’єкти. На приклад, одноразове медичне обладнання стерилізують прискореними електронами після запаковування. Ці електрони рухаються з дуже великими швидкостями. Старі телевізори з електроннопроменевими трубками теж прискорюють електрони.
• В системі GPS не вдавалося досягти метрової точності позиціонування поки не було враховано ефекти описані в цьому тексті.

Що почитати:
Р. Пенроуз “Путь к реальности, или законы, управляющие Вселенной. Полный путеводитель”. Глава 17 “Пространство-время”

Примітка: у формулі для метрики Мінковського час (t) множиться на швидкість світла (c) для того, щоб всі координати часу-простору вимірювалися в однакових одиницях, або, як кажуть фізики, мали однакову розмірність. Це потрібно, бо ми не можемо додавати чи віднімати метри з секундами.

Автор титульного зображення: Brews ohare — Власна робота, GFDL, https://commons.wikimedia.org/w/index.php?curid=3786384
Автор зображення “світлового конусу”: Sakurambo — Власна робота, Суспільне надбання (Public Domain), https://commons.wikimedia.org/w/index.php?curid=2446105